Printk打印内核日志

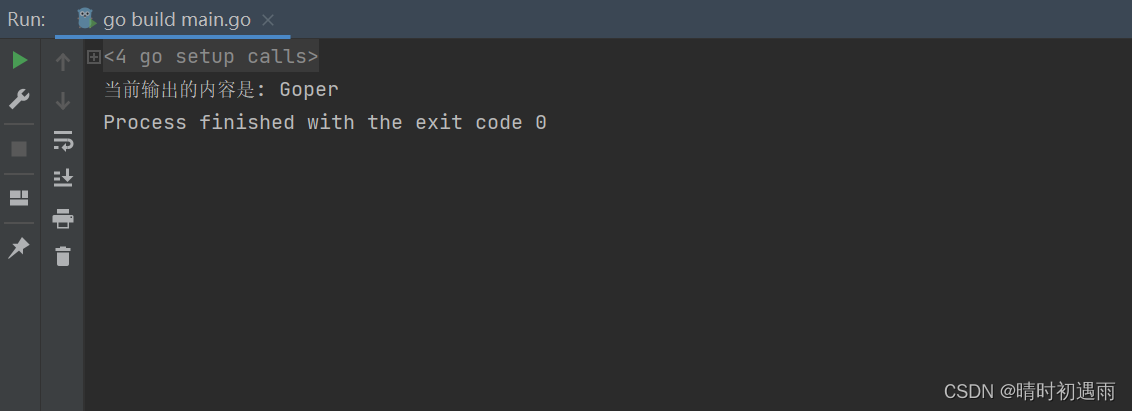
一、背景

Linux 内核中提供了内核日志打印的工具printk。它的使用方式C语言中的printf是类似的。接下来我们介绍一下printk的使用方式。本文以打印Binder中的日志为例，进行演示。

printk的方法声明和日志级别
binder驱动中增加打印代码
android系统中查看日志信息

二、printk方法声明

printk 官方链接

2.1 方法声明

printk(KERN_INFO "Message: %s\n", arg);

KERN_INFO 的位置代表的是要打印的消息级别
printk 的第一个参数 KERN_INFO "Message: %s\n" 整体是一个，格式化字符串
arg 参数的位置，对应占位的值

具体的消息级别有如下集中：

如果缺省消息界别，那就是 KERN_DEFAULT. 具体定义见 include/linux/kern_levels.h

#define KERN_EMERG      KERN_SOH "0"    /* system is unusable */
#define KERN_ALERT      KERN_SOH "1"    /* action must be taken immediately */
#define KERN_CRIT       KERN_SOH "2"    /* critical conditions */
#define KERN_ERR        KERN_SOH "3"    /* error conditions */
#define KERN_WARNING    KERN_SOH "4"    /* warning conditions */
#define KERN_NOTICE     KERN_SOH "5"    /* normal but significant condition */
#define KERN_INFO       KERN_SOH "6"    /* informational */
#define KERN_DEBUG      KERN_SOH "7"    /* debug-level messages */

#define KERN_DEFAULT    KERN_SOH "d"    /* the default kernel loglevel */

2.2 配置可打印消息级别

printk函数所打印的消息，可以通过cat /dev/kmsg 命令试试查看或者通过 dmesg 命令查看历史消息。但是要注意的是 ”并不是所有的级别的消息“ 都会进行输出。这是因为它有一个控制开关：/proc/sys/kernel/printk

上述四个值的含义是：

当前可以消息级别
默认的消息级别
最小消息级别
Boot启动时默认消息级别

因此，我们可以通过控制该文件的值，来管控消息

echo 0 > /proc/sys/kernel/printk 打开消息打印
echo 0 1 4 7 > /proc/sys/kernel/printk 来关消息打印

三、binder驱动中增加打印代码

我们打印一下Android系统binder驱动的读写日志:

static int binder_thread_write(struct binder_proc *proc,
struct binder_thread *thread,
binder_uintptr_t binder_buffer, size_t size,
binder_size_t *consumed)
{
	while (ptr < end && thread->return_error.cmd == BR_OK) {
		int ret;
		if (get_user(cmd, (uint32_t __user *)ptr))
			return -EFAULT;
		ptr += sizeof(uint32_t);
		trace_binder_command(cmd);
		if (_IOC_NR(cmd) < ARRAY_SIZE(binder_stats.bc)) {
			atomic_inc(&binder_stats.bc[_IOC_NR(cmd)]);
			atomic_inc(&proc->stats.bc[_IOC_NR(cmd)]);
			atomic_inc(&thread->stats.bc[_IOC_NR(cmd)]);
		}
		/*print info ： proc.name , proc.id , proc.thread_id, cmd name*/
		printk("%s (%d, %d), %s %s \n" , proc->tsk->comm, proc->pid , thread->pid,__FUNCTION__ , binder_cmd_name(cmd) );
		switch(cmd){
			....
		}
		...
}

读取binder数据时，进行消息打印:
打印消息的时机是针对每一个put_user进行消息打印。

static int binder_thread_read(struct binder_proc *proc,
	struct binder_thread *thread,
	binder_uintptr_t binder_buffer, size_t size,
	binder_size_t *consumed, int non_block)
{
	
	void __user *buffer = (void __user *)(uintptr_t)binder_buffer;
	void __user *ptr = buffer + *consumed;
	void __user *end = buffer + size;
	int ret = 0;
	int wait_for_proc_work;
	if (*consumed == 0) {
		printk("%s (%d, %d), %s %s \n" , proc->tsk->comm, proc->pid , thread->pid,__FUNCTION__ , binder_cmd_name(BR_NOOP) );
		if (put_user(BR_NOOP, (uint32_t __user *)ptr))
			return -EFAULT;
		ptr += sizeof(uint32_t);
	
	}

四、Android系统查看消息

4.1 编译内核

./build/build.sh

将输出的Image.lz4-dtb文件，进行烧录

adb reboot bootloader 

fastboot boot Image.lz4-dtb  //刷入新的镜像文件

4.2 查看消息

4.2.1 查看历史消息

# dmesg
[  315.979119] surfaceflinger (502, 1326), binder_thread_write BC_FREE_BUFFER 
[  315.979142] surfaceflinger (502, 1326), binder_thread_read BR_NOOP 
[  315.995940] ndroid.systemui (1463, 1463), binder_thread_write BC_TRANSACTION 
[  315.996057] ndroid.systemui (1463, 1463), binder_thread_read BR_NOOP 
[  315.996070] ndroid.systemui (1463, 1463), binder_thread_read BR_TRANSACTION_COMPLETE 
[  315.996569] surfaceflinger (502, 1326), binder_thread_write BC_FREE_BUFFER 
[  315.996599] surfaceflinger (502, 1326), binder_thread_read BR_NOOP